Cliquer: a graph theory game.

In February of 2017, I was teaching at Queen’s University.  Part of being a teacher at a University is participating in the community so I attended a talk on directed cliques and their application to dynamical systems.  If that sounds like a mouthful, that’s because it was a pretty dense talk, although the speaker was wonderful at making things clear.  When you’re listening to a good talk about a really hard subject there is a type of payoff that comes from all the mental stimulation.  You get an Idea — maybe not one that is actually about the same topic as the talk.  This talk got me thinking about cliques.

“What is a clique?” I hear you cry.  There is a colloquial English meaning, but like most of mathematics, clique has a very precise and completely different meaning.  The term appears in the field of graph theory.  In graph theory, you have dots, called vertices, connected by lines, called edges.   Edges are thought of as connecting the vertices at their ends.  A clique is a collection of vertices so that all the pairs of vertices are connected by edges.  If there are n vertices in a clique, we call it an n-clique.   Here is a 5-clique:

The 5-clique has 5 vertices and ten edges.  The game we’re going to show you needs you to be able to spot cliques, so lets practice a little.  Take a look at this picture:

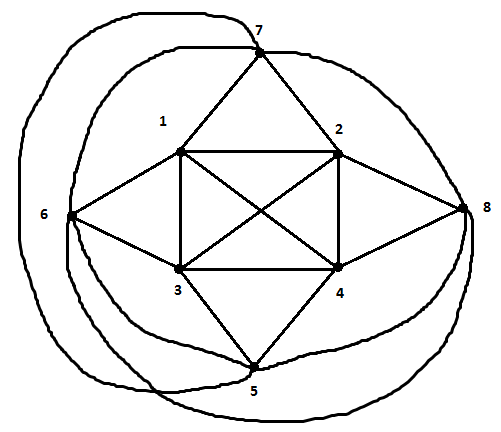
There are 8 vertices, numbered 1-8, and the connections are shown in the picture as lines, some of which are curved. If you were to count the edges, you would find there are 18 of them.   Following the definition of clique, above, there are 18 2-cliques in this graph. It is not a coincidence that this is the same number as the number of edges. A 2-clique is just an edge between two vertices, and if we choose the two vertices that are joined by an edge, then they are both connected to each other and satisfy the definition of a clique.

Consider the 3-cliques, if any, in this graph.  Here the counting becomes a little trickier. For three vertices to form a 3-clique, they all must be connected to each other. If we consider vertices 1, 2, and 3, we can see that 1 shares an edge with 2, 3 shares an edge with 1, and 3 shares an edge with 2; thus those three vertices form a 3-clique.  In graph theory we call this a triangle. Notice that I’m redefining “triangle” in the context of this document, but everywhere else I talk about a triangle I really mean the standard one we all learned in grade school. It turns out that if you count carefully, there are actually 16 triangles (3-cliques) embedded in this graph.  Can you find them?

When we look for 4-cliques, there are only two! 1, 2, 3, and 4 form a 4-clique, and 5, 6, 7, and 8 form a 4-clique as well.  Check that those groups of four vertices have all six possible edges.   Are there any five cliques? I couldn’t find any. Hopefully we have an idea of cliques that is pretty solid by this point.  This means we’re ready for the game.

The Game

Cliques are actually a pretty important aspect of network analysis, for topics like modeling disease spread or user adoption of new products on the market. In terms of what I want to write about, cliques are cool because you can make a game out of them, something I did while I was teaching a game theory class.  The name of this game is Cliquer and, as you probably guessed, cliques are the backbone upon which the game is built.

Cliquer is a super simple game to learn, and it turns out to be as least as mathematically rich as Nim and similar takeaway games. What you need is a piece of paper (or some flat surface on which you can draw), some drawing device, and at least two people. You start by drawing at least seven vertices (dots) on the paper.  There are no rules about where you put them.

A move consists of drawing an edge between two vertices that are not already joined by an edge.   That new edge cannot cross an existing edge or vertex.  That’s it.  There is only one rule about how to make a move in this game: connect two vertices without drawing over something else.  The game is over when no more edges can be drawn. Turns out, this one rule still makes the game complicated enough that every mathematician I have shown this to has gone, “Wow, nice game!” So where do cliques come into this process? Cliques are used to score the game.

Scoring in Cliquer

The rules for scoring are as follows.  A player gets one point for completing a 2-clique. Notice that this guarantees that each person gets at least one point every time it is their turn, assuming there are still moves to be made.  If, by drawing an edge, a player completes a 3-clique, the player scores 3 points.  If, by drawing an edge, a player completes a 4-clique, the player scores 5 points. A move consists of adding one edge, but you get the score for every clique that is completed.

Let’s work through an example game of Cliquer.  The rules say a game needs at least seven dots, but we are only going to use four to keep the example to a reasonable size.

Put down four dots in any arrangement you see fit, something like the picture here:

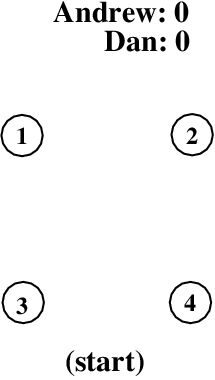
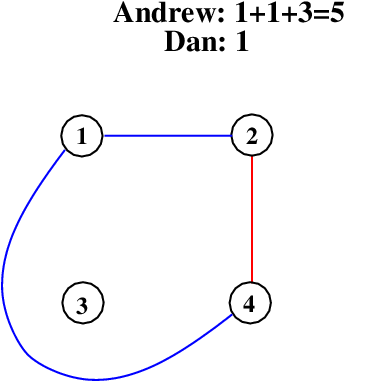
It often helps to label the vertices with numbers, or letters, or whatever your labeling preference, but use something to distinguish the vertices so that everyone knows what is going on. For this example, I’ll be playing against Dan, and I’m going to go first and I will connect vertices 1 and 2.

That means I get one point, for completing a 2-clique.  Dan then draws an edge from 2 to 4 and gets one point.

I then connect 4 and 1 with a curved line that goes around the outside of 3.  It could have gone inside, but this is fine.  I score one for my edge and three for completing the clique 1-2-4.

Dan then connects 3 and 4 and gets one more point.  It’s not looking good for him.

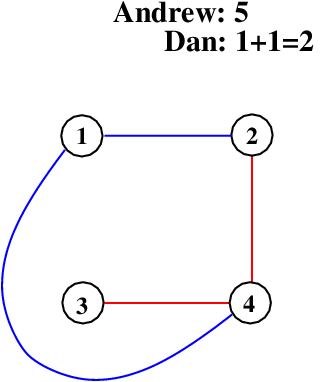
I connect one and three, getting an edge and also completing the clique 1-3-4.  I’m up to nine points.

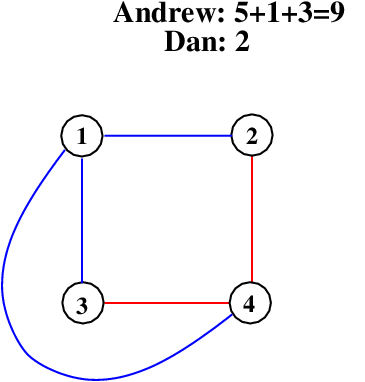
Since there is only one move left, Dan connects 2 and 3.  This is not only an edge, it finishes the 3-cliques 1-2-3 and 2-3-4 and the 4-clique with vertices 1-2-3-4.  This gives Dan 12 points and he comes from way behind to win.

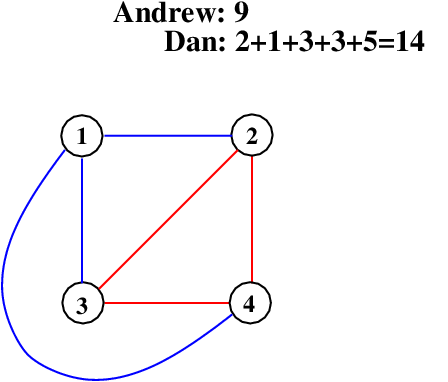
After that I can see that there are no more moves, since all pairs of vertices now share an edge. The game is over, and Dan wins 14 to 9.  This example shows how important it is that you can complete multiple cliques with one move.  Some of you may be thinking, “if different moves had been made, would the result be different?” The answer, in this case, is no! Why? It has to do with the number of vertices,  and I will look into that in the next blog about Cliquer, and some of the underlying mathematics.  The way the four-vertex game comes out is one of the reasons the rules say “7 or more.”

I will end with the following thoughts. Cliquer has barely been analyzed by myself and some of my more interested students. What is the right strategy to win? Is it better to give triangles up first, or claim as many as you can in the beginning? Lots of questions! There are other variations of Cliquer that Dan and I’ve thought about as well, and that will probably yield a third post about the game.

To hold you until next time here are a couple of Cliquer boards and a puzzle about them. This problem uses one of the variations of Cliquer: you can only draw straight lines between vertices. With that restriction, answer the following question: is the top score possible on one of these boards higher than the top score on the other?

This is Andrew of Dan and Andrew’s Game Place. Let me know what you think about this post in the comments. If you get ideas from this, give us a pointer!